Sample Problems
1) The World Series is a best-of-seven contest. (Two baseball teams play up to 7 games against each other. As soon as 1 team has won 4 games, the contest is over.) If teams A and B play in the series, a sequence of winners for the games played might be AAAA or ABBABAB, but could not be AAAAB.
How many different sequences of winners for the games of a World Series between Team A and Team B are possible?
Show answer
Answer
70
Suppose that a World Series is completed leading to an extended series where extra exhibition games are played (between the same two teams) after the series has been won. These exhibition games are always to be won by the team that lost the official World Series and are to continue until that losing team also has a total of 4 wins. In this way, if the results of the World Series read ABAABA, then the results of the extended series read ABAABABB.
The sequence of results for the extended series is just an arrangement of 4 copies of the letter A and 4 copies of the letter B. There are 8C4 = 8x7x6x5/4x3x2x1 = 70 such arrangements. (We may choose 4 positions for the letter A from 8 possible positions.)
Each sequence of results for the extended series determines exactly one possible sequence of results for the World Series (by omitting the exhibition games).
2) Two CUNY math professors arrange to meet to prepare a test. Each will arrive at a random time between 1:00 P.M. and 2:00 P.M. and will wait up to 15 minutes for the other before leaving.
What is the probability that the meeting takes place?
Show answer
Answer
7⁄16
Associate each arrival time between 1:00pm and 2:00pm with a real number
r such that 0 < r < 1. The number
r represents the part of the hour that has elapsed before the arrival.
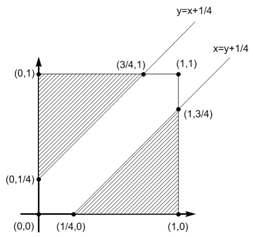
In this way the arrival times of the two professors determine a coordinate pair (x,y) that corresponds to a point in the unit square with 0 < x < 1,0 < y < 1.
The pair (x,y) corresponds to a situation where the professors fail to meet if either y > x +
1⁄
4 or x > y +
1⁄
4 (see right).
In the first of these cases the point (x,y) lies in the triangle that lies above the line y = x +
1⁄
4. The area of this triangle is
1⁄
2 x
3⁄
4 x
3⁄
4 =
9⁄
32. Similarly, in the second case, the point (x,y) lies in the triangle with area
9⁄
32 that lies below the line x = y +
1⁄
4. We deduce that the probability that the professors do not meet is
9⁄
32 +
9⁄
32 =
9⁄
16. Therefore the probability that they do meet is
7⁄
16.
3) Alice and Bob are bored and want to play a game. "I have an idea," Alice chimes in. "How about you flip this coin 2009 times and I'll flip it 2010 times and whoever gets more Heads wins?"
Bob replies, "No, that's not fair! You're probably going to win since you get more flips!"
"Fine!" answers Alice. "How about this? You flip the coin 2009 times and I'll flip it 2010 times and if I get more Heads, I win. If you get more Heads, you win. And, if there's a tie, we'll say that you win too." Bob shrugs his shoulders and agrees to play.
What's the probability that Alice wins the game? Prove your answer.
Show answer
Answer
1⁄2
1st Proof: Alice flips the coin more often than Bob, so either she must end up with more Heads or with more Tails than Bob. She cannot, however, end up with more Heads and more Tails because she only flips the coin once more than Bob. We deduce that either Alice gets more Heads or she gets more Tails. Since these events are equally likely, both have probability 1⁄2.
2nd Proof: Suppose that Alice and Bob begin by flipping the coin N=2009 times each. Let p be the probability that Alice gets more Heads than Bob and let q be the probability that both Alice and Bob get an equal number of Heads. Then 2p+q=1. Alice then flips the coin an (N+1)st time. For Alice to have more Heads, she either had more Heads after the initial Nth flips or an equal number of Heads after the initial flips and her (N+1)st flip must come up Heads. That is, the probability of Alice winning is p+q(1/2). Since 2p+q=1, p+q(1/2)=1/2.